常见数学条件的给出方式
前言
研究各种常见的数学条件的给出方式,能帮助我们更好的理解题意,更快的入题。
相关阅读
- 1、例说学习方法的改造和提升
- 2、分式型函数相关
- 3、变量集中
- 4、齐次式
知识点列举
案例:集合的包含关系给出方式
\(A\subseteq B\)
\(\Longleftrightarrow\) \(A\cap B=A\)
\(\Longleftrightarrow\) \(A\cup B=B\)
\(\Longleftrightarrow\) \(C_UB\subseteq C_UA\)
\(\Longleftrightarrow\) \(A\cap(C_UB)=\varnothing\)
案例:命题真假的给出方式
- 若\(p\land q\)为假,则\(p\)和\(q\)中至少有一个为假; 若\(p\lor q\)为真,则\(p\)和\(q\)中至少有一个为真;
- 若\(p\land q\)为真,则\(p\)和\(q\)都为真; 若\(p\lor q\)为假,则\(p\)和\(q\)都为假;
- 若\(\neg p\land q\)为真,则\(\neg p\)和\(q\)都为真,即\(p\)为假且\(q\)为真;
- 若\(\neg p\lor q\)为假,则\(\neg p\)和\(q\)都为假,即\(p\)为真且\(q\)为假;
- “若\(p\lor q\)为真命题,\(p\land q\)为假命题”,则意味着\(p\)、\(q\)必然一真一假,需要分类讨论:\(p\)真\(q\)假;或\(p\)假\(q\)真;
案例:正切值的给出方式
- 限定条件以简单变形形式给出,如已知\(tan\theta=2\),求\(\cfrac{sin2\theta-\cos^2\theta}{1+\sin^2\theta}\)的值。[1]
- 已知\(\cfrac{\sin\theta-\cos\theta}{\sin\theta+\cos\theta}=2\),求\(\cfrac{\sin2\theta-\cos^2\theta}{1+\sin^2\theta}\)的值。
- 已知\(\theta\)角的终边过点\((4a,-3a)(a>0)\),求\(\cfrac{\sin2\theta-\cos^2\theta}{1+\sin^2\theta}\)的值。
- 已知\(\theta\)角的终边在直线\(3x+4y=0\)上,求\(\cfrac{\sin2\theta-\cos^2\theta}{1+\sin^2\theta}\)的值。
- 已知如图,\(\tan\theta=AT\),求\(\cfrac{\sin2\theta-\cos^2\theta}{1+\sin^2\theta}\)的值。
- 已知\(\sin\theta=2\cos\theta\),求\(\cfrac{\sin2\theta-\cos^2\theta}{1+\sin^2\theta}\)的值。
- 已知\(\tan2\theta=-\cfrac{4}{3}\),求\(\cfrac{\sin2\theta-\cos^2\theta}{1+\sin^2\theta}\)的值。
- 若倾斜角为\(\theta\)的直线\(l\)与曲线\(y=x^4\)相切于点\((1,1)\),求\(\cfrac{\sin2\theta-\cos^2\theta}{1+\sin^2\theta}\)的值。
- 已知\(\sin(\cfrac{\pi}{6}-\theta)=\cos(\cfrac{\pi}{6}+\theta)\),求\(\cfrac{\sin2\theta-\cos^2\theta}{1+\sin^2\theta}\)的值。
- 已知\(sin(\pi-\theta)=2sin(\cfrac{\pi}{2}+\theta)\),求\(\cfrac{sin2\theta-cos^2\theta}{1+sin^2\theta}\)的值。
- 已知直线\(2x-y-1=0\)的倾斜角为\(\theta\),求\(\cfrac{\sin2\theta-\cos^2\theta}{1+\sin^2\theta}\)的值。
- 已知点\((\theta,0)\)为函数\(f(x)=sinx+2cosx\)图像的一个对称中心,求\(\cfrac{\sin2\theta-\cos^2\theta}{1+\sin^2\theta}\)的值。
- 已知直线\(l_1:x\cos\theta+2y=0\)与直线\(l_2:3x+y\sin\theta+3=0\)垂直,求\(\cfrac{\sin2\theta-\cos^2\theta}{1+\sin^2\theta}\)的值。
- 已知直线\(l_1:x\cos\theta+2y=0\)与直线\(l_2:x\sin\theta+3y+3=0\)平行,求\(\cfrac{\sin2\theta-\cos^2\theta}{1+\sin^2\theta}\)的值。
- 以双曲线的渐近线的夹角形式给出[2]
案例:解三角形中的条件的给出方式
已知\(\triangle ABC\)的内角\(A\),\(B\),\(C\)的对边为\(a\),\(b\),\(c\),_____________,\(A=\cfrac{\pi}{3}\),\(b=\sqrt{2}\),求\(\triangle ABC\)的面积;
分析:由①\(b^2+\sqrt{2}ac=a^2+c^2\)可得,\(\cos B=\cfrac{\sqrt{2}}{2}\),则\(B=\cfrac{\pi}{4}\);
由②\(a\cos B=b\sin A\)可得,\(\sin A\cos B=\sin B\sin A\),即\(\sin B=\cos B\),则\(B=\cfrac{\pi}{4}\);
由③\(\sin B+\cos B=\sqrt{2}\)可得,\(\sqrt{2}sin(B+\cfrac{\pi}{4})=\sqrt{2}\),即\(sin(B+\cfrac{\pi}{4})=1\),则\(B=\cfrac{\pi}{4}\);
故不论选择哪一个,通过不同的变形,都会得到条件\(B=\cfrac{\pi}{4}\),故原问题等价于:
已知\(\triangle ABC\)的内角\(A\),\(B\),\(C\)的对边为\(a\),\(b\),\(c\),\(B=\cfrac{\pi}{4}\),\(A=\cfrac{\pi}{3}\),\(b=\sqrt{2}\),求\(\triangle ABC\)的面积;
则由正弦定理\(\cfrac{a}{\sin A}=\cfrac{b}{\sin B}\),可得\(a=\sqrt{3}\),
故\(S_{\triangle ABC}=\cfrac{1}{2}ab\sin C=\cfrac{1}{2}ab\sin (A+B)=\cfrac{1}{2}\times\sqrt{2}\times\sqrt{3}\times\sin(\cfrac{\pi}{4}+\cfrac{\pi}{3})\)
\(=\cfrac{3+\sqrt{3}}{4}\);
案例:直线斜率的给出方式
- 利用斜率\(k=\tan\alpha\)的定义;
- 利用过两点的坐标,
- 利用导函数\(k=f'(x_0)\)给出,
如若倾斜角为\(\alpha\)的直线\(l\)与曲线\(y=x^4\)相切于点\((1,1)\),则\(k=tan\alpha=y'|_{x=1}=4x^3|_{x=1}=4\)。
- 利用函数的切线的方向向量的坐标。
案例 : 圆的给出方式
- 定义式:\(|OA|=r\)
- 标准式方程:\((x-a)^2+(y-b)^2=r^2\);
- 一般式方程\(x^2+y^2+Dx+Ey+F=0(D^2+E^2-4F>0)\);
- 直径式方程\((x-x_1)(x-x_2)+(y-y_1)(y-y_2)=0\)(其中圆的直径的端点是\(A(x_1,y_1)\)、\(B(x_2,y_2)\))。
- 参数式:\(x=r\cdot cos\theta,y=r\cdot sin\theta\)或\((r\cdot cos\theta,r\cdot sin\theta)\)
- 极坐标式:\(\rho=3,\theta\in [0,2\pi)\)
- 向量式:已知点\(M\)为曲线上的动点,点\(A,B\)为两个定点,且满足关系\(\overrightarrow{MA}\cdot\overrightarrow{MB}=0\),则点\(M\)的轨迹方程是圆。[3]
案例 :三点共线的给出方式或证明思路
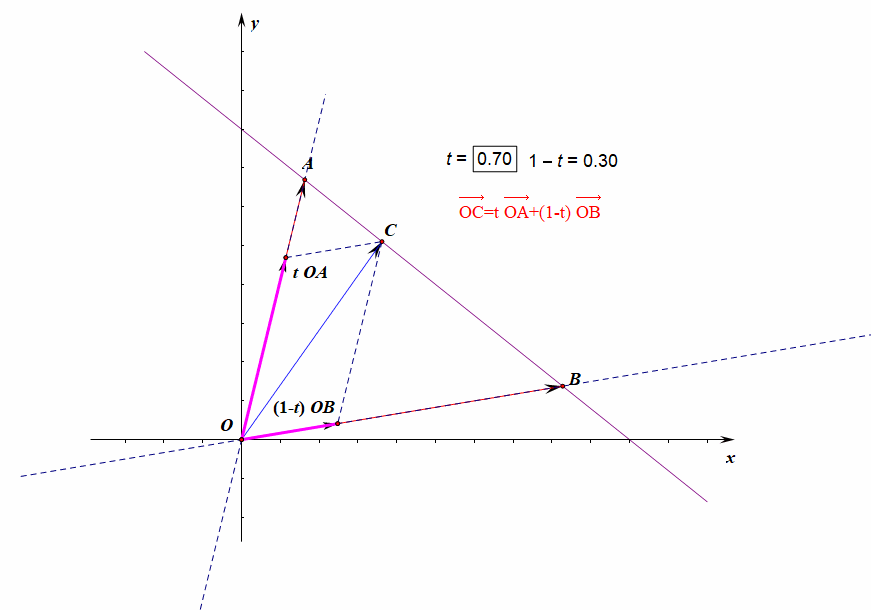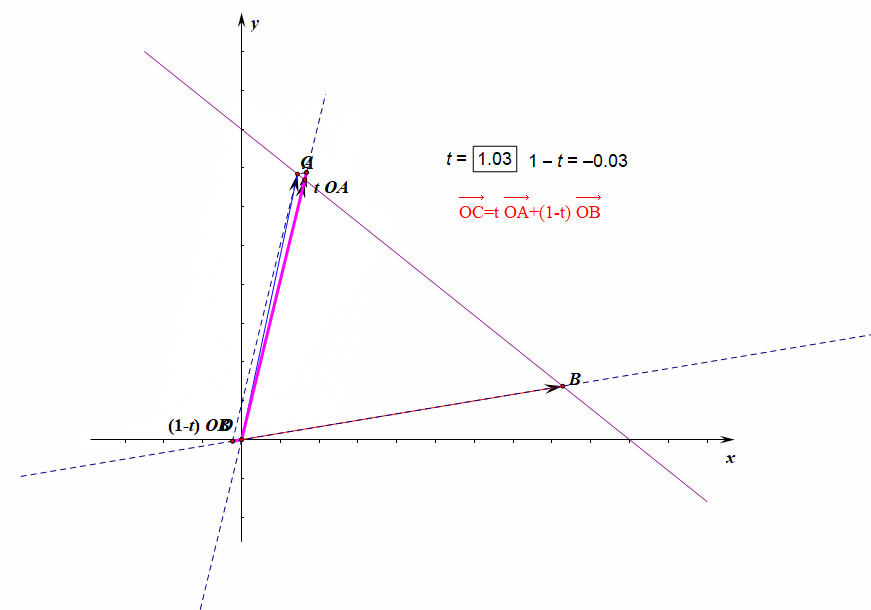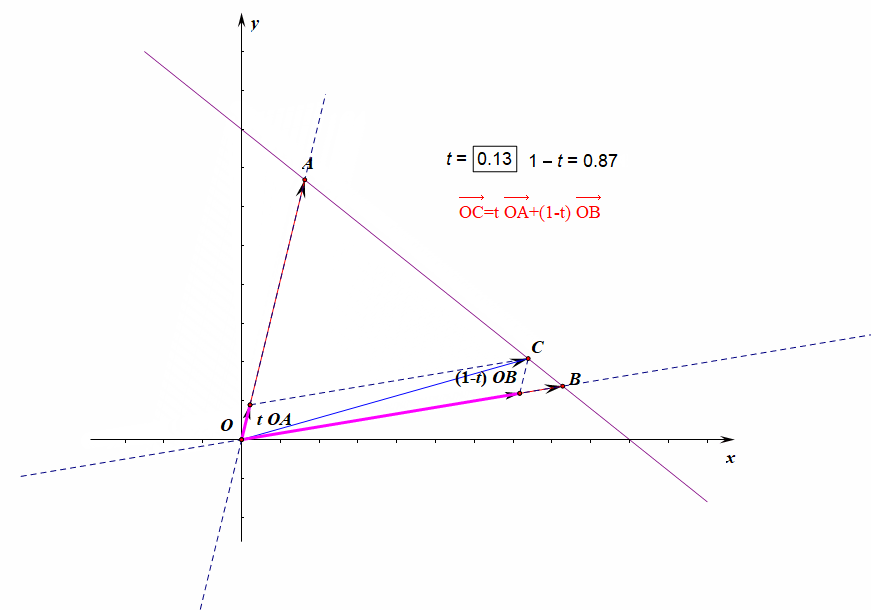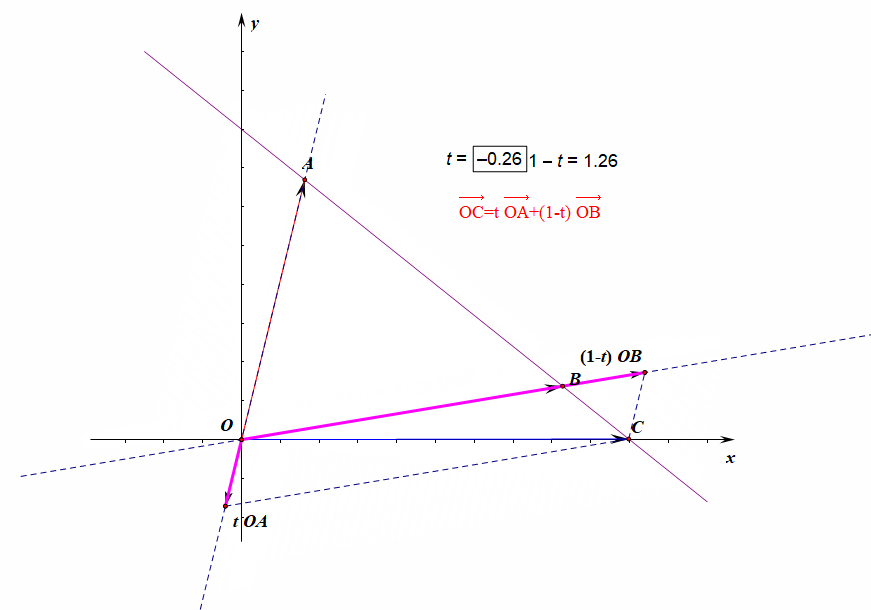
- 向量表示形式:\(\overrightarrow{OC}=\lambda\overrightarrow{OA}+(1-\lambda)\overrightarrow{OB}\)[4]或\(\overrightarrow{AB}//\overrightarrow{AC}\)
- 距离表示形式:\(|AB|+|BC|=|AC|\)
- 斜率表示形式:\(k_{AB}=k_{AC}\)
案例 : 等差数列的给出方式
- 直接给出:\(a_{n+1}-a_n=3\)
- 变形给出:\(a_{n+1}=a_n+3\)
- 运算给出:\((a_{n+1}+a_n)(a_{n+1}-a_n)=0\),\(a_n>0\)
- 向量给出:\(\overrightarrow{P_nP_{n+1}}=(1,a_{n+1}-a_n)=(1,3)\)
案例 :对称中心的给出方式
- 直接给出:如函数\(f(x)=sin(x+\phi)\)的对称中心是\((\cfrac{\pi}{3},0)\)
- 间接给出:如函数\(f(x)=sin(x+\phi)\)过点是\((\cfrac{\pi}{3},0)\),则点\((\cfrac{\pi}{3},0)\)必是函数的对称中心
- 间接给出:如函数\(f(x)=sin(x+\phi)\),满足\(\int_{0}^{\frac{2\pi}{3}}f(x)\, dx=0\),则点\((\cfrac{\pi}{3},0)\)必是函数的对称中心
- 隐晦给出:如函数满足\(f(x)+f(\cfrac{2\pi}{3}-x)=0\),则点\((\cfrac{\pi}{3},0)\)必是函数的对称中心
案例 :相等关系的给出方式
- 直接给出:如\(f(2)=4\),
- 以不等关系给出:如\(2x\leq f(x)\leq \cfrac{1}{2}x^2+2\)对任意\(x\in R\)恒成立,则赋值可得\(4\leq f(2)\leq 4\),即\(f(2)=4\);
再比如\(|k|\leq 0\),即等于给出\(k=0\);\((m-1)^2\leq 0\),即等于给出\(m=1\);
案例 :不等式的解的给出方式
- 直接给出:\(x=1\)是不等式\(x^2-2x+a\leq 0\)的解,求\(a\)的范围。
- 间接给出:集合\(\{1\}\)是不等式\(x^2-2x+a\leq 0\)的解集\(A\)的真子集,求\(a\)的范围。
- 间接给出:\(x=1\)满足不等式\(x^2-2x+a\leq 0\)是真命题,求\(a\)的范围;\(x=1\)满足不等式\(x^2-2x+a> 0\)是假命题,求\(a\)的范围。
- 隐晦给出:集合\(A=\{x\mid x^2-2x+a>0\}\),\(1\notin A\),求\(a\)的范围;
案例 :函数的性质的给出方式
案例 :ω的给出方式
- 直接给出:函数\(f(x)=2sin(2x+\cfrac{\pi}{3})\)的图像的横坐标缩短为原来的\(\cfrac{1}{3}\),即新的\(\omega=3\);
- 间接给出:\(f(x)=2sin(x+\cfrac{\pi}{3})\)的图像的横坐标扩大了\(2\)倍,即图像的横坐标扩大为原来的\(3\)倍,即新的\(\omega=\cfrac{1}{3}\);
- 间接给出:\(f(x)=2tan\omega x(\omega>0)\)的图像的相邻两支截直线\(y=2\)所得的线段长为\(\cfrac{\pi}{2}\),即\(T=\cfrac{\pi}{\omega}=\cfrac{\pi}{2}\),则\(\omega=2\);
- 间接给出:函数\(f(x)=2sin(\omega x+\cfrac{\pi}{3})\)的图像的相邻的两个最高(低)点之间的距离是3,即\(T=3\),求得\(\omega=\cfrac{2\pi}{3}\);
- 间接给出:函数\(f(x)=2sin(\omega x+\cfrac{\pi}{3})\)的图像的相邻的最高点和最低点之间的距离是5,由勾股定理求得\(\cfrac{T}{2}=3\),则\(\omega=\cfrac{\pi}{3}\);
- 间接给出:函数\(f(x)=2sin(\omega x+\cfrac{\pi}{3})\)的图像的相邻的两个零点之间的距离是3,即\(\cfrac{T}{2}=3\),则\(\omega=\cfrac{\pi}{3}\);
- 间接给出:函数\(f(x)=2sin(\omega x+\cfrac{\pi}{3})\)的图像的相邻的两条对称轴之间的距离是3,即\(\cfrac{T}{2}=3\),则\(\omega=\cfrac{\pi}{3}\);
- 间接给出:函数\(f(x)=2sin(\omega x+\cfrac{\pi}{3})\)的图像的相邻对称轴和零点之间的距离是3,即\(\cfrac{T}{4}=3\),则\(\omega=\cfrac{\pi}{6}\);
- 间接给出:函数\(f(x)=2sin(\omega x+\cfrac{\pi}{3})\)的图像的相邻的最高点和零点之间的距离是\(2\sqrt{2}\),由勾股定理求得\(\cfrac{T}{4}=2\),则\(\omega=\cfrac{\pi}{4}\);
案例 :二次函数的系数的给出方式
- 直接给出:已知二次函数\(f(x)=x^2-ax+a(a>0,x\in R)\)的系数\(a=?\),
- 间接给出:已知二次函数\(f(x)=x^2-ax+a(a>0,x\in R)\),有且只有一个零点,则\(\Delta =0\),解得\(a=4\);
- 间接给出:已知二次函数\(f(x)=x^2-ax+a(a>0,x\in R)\),\(f(x)\)的值域为\([0,+\infty)\),则\(\Delta =0\),解得\(a=4\);
案例 :数列的周期性的给出方式:
- \(a_{n+2}=a_n\)或\(a_{n+2}-a_n=0\);则数列的\(T=2\);
分析:类比\(f(n+2)=f(n)\),再类比\(f(x+2)=f(x)\);
- \(a_{n+2}=-a_n\)或 \(a_{n+2}+a_n=0\);则数列的\(T=4\);
分析:类比\(f(n+2)=-f(n)\),再类比\(f(x+2)=-f(x)\);
- \(a_{n+2}=\cfrac{k}{a_n}\)或\(a_{n+2}\cdot a_n=k\);\(k\)为常数;等积数列,则数列的\(T=4\);
分析:类比\(f(n+2)=\cfrac{k}{f(n)}\),再类比\(f(x+2)=\cfrac{k}{f(x)}\);
- \(a_{n+2}=a_{n+1}-a_n\)或\(a_{n+2}+a_n=a_{n+1}\);则数列的\(T=6\);
分析:类比\(f(n+2)=f(n+1)-f(n)\),再类比\(f(x+2)=f(x+1)-f(x)\);
- \(a_{n+1}=(-1)^n(a_n+1)\);通过计算前面的有限项得到周期;
案例 :分段函数的给出方式
- 直接给出:函数\(f(x)=\begin{cases}2x+a,&x< 1\\-x-2a,&x\ge 1 \end{cases}\).
- 间接给出:已知奇函数\(f(x)\)满足\(x>0\)时,\(f(x)=2^x\),则利用奇偶性可知函数\(f(x)=\left\{\begin{array}{l}{2^x,x>0}\\{0,x=0}\\{-2^{-x},x<0}\end{array}\right.\)
- 用程序框图给出:
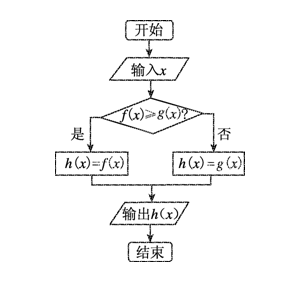
案例 :线段等分点的向量给出方式
二等分点(中点):\(\overrightarrow{OA}=-\overrightarrow{OB}\),或\(\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{0}\),则点\(O\)是\(AB\)的中点;即\(|OA|=|OB|\);
三等分点:\(\overrightarrow{OA}=-2\overrightarrow{OB}\),或\(\overrightarrow{OA}+2\overrightarrow{OB}=\overrightarrow{0}\),则点\(O\)是\(AB\)的靠近\(B\)的三等分点;即\(|OA|=2|OB|\);
相关变形技巧:\(\overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}=\vec{0}\),
将其系数做恰当的拆分得到,\((\overrightarrow{OA}+\overrightarrow{OC})+2(\overrightarrow{OB}+\overrightarrow{OC})=\vec{0}\),
如图即\(2\overrightarrow{OD}=-4\overrightarrow{OE}\),即\(\overrightarrow{OD}=-2\overrightarrow{OE}\),
即可知点\(O\)一定在\(\Delta ABC\)的中位线\(DE\)上,且在中位线上靠近点\(E\)的三等分点处。
四等分点:\(\overrightarrow{OA}=-3\overrightarrow{OB}\),或\(\overrightarrow{OA}+3\overrightarrow{OB}=\overrightarrow{0}\),则点\(O\)是\(AB\)的靠近\(B\)的四等分点;即\(|OA|=3|OB|\);
案例 :三角形的重心的给出方式
- 直接给出:点\(O\)是\(\triangle ABC\)的重心;
- 间接给出:点\(O\)是\(\triangle ABC\)的边\(BC\)的中线上的靠近\(BC\)的三等分点;
- 间接给出:\(\overrightarrow{OA}=-2\overrightarrow{OB}\),点\(O\)是中位线\(DE\)的三等分点,是\(\triangle BCD\)的重心;
- 间接给出:\(\overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}=\vec{0}\),点\(O\)是中位线\(DE\)的三等分点,是\(\triangle BCD\)的重心;
- 间接给出:\(\overrightarrow{AB}+\overrightarrow{AC}=3\overrightarrow{AD}\),点\(D\)是\(\triangle ABC\)的重心;
案例:长度型几何概型的事件的给出方式
在区间\([-5,5]\)上随机取一个数\(k\),则事件\(A:\)“直线\(y=kx\)与圆\((x-5)^2+y^2=9\)相交”发生的概率为____________。
则①以直线和圆相交的方式给出;
比如,在区间\([-1,1]\)上随机取一个数\(k\),则事件“直线\(y=kx\)与圆\((x-5)^2+y^2=9\)相交”发生的概率为____________.
②以定义域的方式给出;
比如,记函数\(f(x)=\sqrt{6+x-x^2}\)的定义域为\(D\),在区间\([4,5]\)上随机取一个数\(x\),则\(x\in D\)的概率为______________。
③以函数单调递增的方式给出,比如使得函数\(f(x)=x^3+mx^2+3x\)在\(R\)上单调递增的概率,即求\(f'(x)\ge 0\)的解集;
④以不等式的解集形式给出,比如\(A=\{x\mid \cfrac{x-1}{2-x}>0\}\);
⑤以三角不等式的形式给出,比如\(A:sinx+\sqrt{3}cosx\leq 1\);
详解:\(\cfrac{sin2\theta-cos^2\theta}{1+sin^2\theta}=\cfrac{2sin\theta cos\theta-cos^2\theta}{2sin^2\theta+cos^2\theta}\)
\(=\cfrac{2tan\theta-1}{2tan^2\theta+1}=\cfrac{2\times 2-1}{2\times2^2+1}=\cfrac{1}{3}\)
【解后反思】分子分母都是关于\(sin\theta\)和\(cos\theta\)的二次齐次式时,给分子分母同除以\(cos^2\theta\),转化为关于\(tan\theta\)的一元函数问题来求解,代值运算即可。 ↩︎(2018宝鸡市二检)双曲线\(\cfrac{y^2}{4}-x^2=1\)的渐近线所夹的角中的锐角为\(\alpha\),求\(cos2\alpha\)的值。
分析:由题目可以知道,其渐近线为\(y=\pm 2x\),
取其一\(y=2x\),则其倾斜角为\(\theta\),可知\(tan\theta=2\),
求\(tan\alpha\)的思路之一:
又知道\(\theta+\cfrac{\alpha}{2}=\cfrac{\pi}{2}\),则\(\theta=\cfrac{\pi}{2}-\cfrac{\alpha}{2}\),带入上式得到,
\(tan\theta=tan(\cfrac{\pi}{2}-\cfrac{\alpha}{2})=cot\cfrac{\alpha}{2}=2\),即\(cot\cfrac{\alpha}{2}=2\),
则\(tan\cfrac{\alpha}{2}=\cfrac{1}{2}\),由\(tan\alpha=\cfrac{2tan\cfrac{\alpha}{2}}{1-tan^2\cfrac{\alpha}{2}}\)得到,\(tan\alpha=\cfrac{4}{3}\)。
求\(tan\alpha\)的思路之二:
用三角函数的定义,在\(y=2x\)上取点\((1,2)\),\(tan\cfrac{\alpha}{2}=\cfrac{1}{2}\),
由\(tan\alpha=\cfrac{2tan\cfrac{\alpha}{2}}{1-tan^2\cfrac{\alpha}{2}}\)得到,\(tan\alpha=\cfrac{4}{3}\)。
到此,题目转化为已知\(tan\alpha=\cfrac{4}{3}\),求\(cos2\alpha=?\)的值。
\(cos2\alpha=\cfrac{cos^2\alpha-sin^2\alpha}{cos^2\alpha+sin^2\alpha}=\cfrac{1-tan^2\alpha}{1+tan^2\alpha}=-\cfrac{7}{25}\)。 ↩︎引申:若\(\overrightarrow{MA}\cdot\overrightarrow{MB}>0\),则点\(M\)在以\(AB\)为直径的圆外部;
若\(\overrightarrow{MA}\cdot\overrightarrow{MB}<0\),则点\(M\)在以\(AB\)为直径的圆内部; ↩︎

 有意识总结常见数学条件的给出方式,有助于我们更好的理解数学内容。
有意识总结常见数学条件的给出方式,有助于我们更好的理解数学内容。